해당 게시물은 "혁펜하임의 AI DEEP DIVE"를 수강하고 작성되었습니다.
MSE를 loss함수로 쓸 수는 없을까?
강아지 사진일 때 출력 $q$가 1이 나온다면 $(q-1)^2$즉 MSE를 loss함수로 사용해서 이걸 minimize하면 되지 않을까?
그럴듯한 생각이다.
그렇다면 $(q-1)^2$를 minimize 하는 것과 $-\log{q}$를 minimize 하는 것을 비교해 보자.
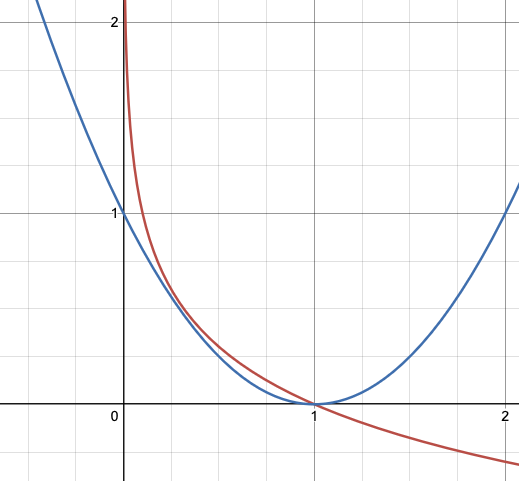
위 그래프에서 파란색이 $(q-1)^2$이며 빨간색이 $-\log{q}$이다.
여기서 알 수 있는 것은, 만약 강아지 사진을 고양이 사진이라고 했을 때 즉, $q=0$일때 loss값을 비교해 보면 $-\log{q}$가 훨씬 크다는 것이다.
$-\log{q}$가 아닌걸 아니라고 강력하게 (민감하게) 주장할 수 있는 loss함수인 것이다.
만약 입력 데이터 1이 $weight=w$이고 $bias=0$, 마지막으로 sigmoid function을 거쳐 출력된다고 가정하자.
이때 loss function을 $(q-1)^2$로 잡으면 결과값은 $(\frac{1}{1+e^{-w}}-1)^2$
loss function을 $-\log{q}$로 잡으면 결과값은 $-\log{\frac{1}{1+e^{-w}}}$ 이다.
우리는 loss가 최소가 되는 점을 찾고자 하는데, local minimum에 빠지지 않기 위해서는 최대한 아래로 볼록한 함수(convex)가 찾기 편할 것이다. (위 아래로 꿀렁거리면 local minimum에 빠지기 쉽상이다.)
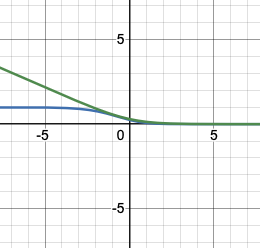
그래프로 확인해 보자. 파란색 그래프가 $(\frac{1}{1+e^{-w}}-1)^2$, 빨간색 그래프가 $-\log{\frac{1}{1+e^{-w}}}$이다.
파란색 그래프는 non-convex하며 빨간색 그래프는 convex하다. 무엇이 gradient descent 시 minumum을 찾기가 쉽겠는가?
당연히 $-\log{\frac{1}{1+e^{-w}}}$가 더 쉽다는 결론이 나온다.
따라서 우리는 MSE를 loss로 사용하기 보다는 log function을 loss로 사용하는 것을 선호하는 것이다.
'AI' 카테고리의 다른 글
| Softmax를 이용한 다중 분류 (0) | 2024.09.05 |
|---|---|
| 딥러닝 학습의 본질 (MLE) (0) | 2024.09.05 |
| Sigmoid를 이용한 이진 분류, Logistic Regression (0) | 2024.09.04 |
| 선형 분류 & 퍼셉트론 (2) | 2024.09.04 |
| Backpropagation (0) | 2024.09.03 |
