Random Forest의 기초가 되는 의사결정트리 (Decision Tree)에 대해서 알아본다.
의사결정트리는 지도학습 방법 중, "분류" 문제를 푸는데 사용된다.
데이터가 존재할 때, 스무고개를 통해 그 데이터가 어떤 class에 속하는지 맞추는 예시와 상당히 유사하다.
그렇다면, 의사결정트리의 구성요소에 대해 설명한다.
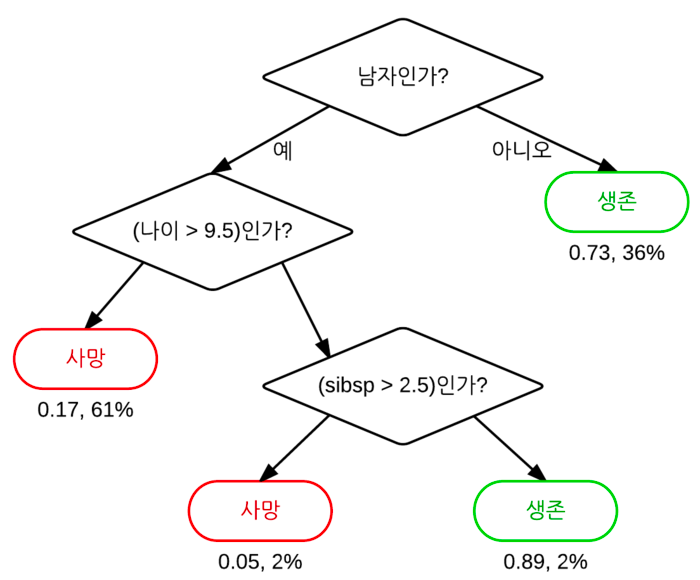
위와 같은 그림에서 각 노드의 명칭은 아래와 같다.
- 맨 처음 분류 기준을 Root Node
- 중간 분류 기준을 Intermediate Node
- 맨 마지막 노드를 Terminal Node 혹은 Leaf Node
이제, 완성된 의사결정트리를 보고 역으로 그 원리에 대해 설명하겠다.
위 그림은 depth=2 상태로 완성된 의사결정트리이다.
여기서 Root Node와 Intermediate Node에 petal width (cm) 에 대한 조건이 존재한다. 이 조건은 학습을 통해 모델이 설정한 조건이다. 이러한 조건을 어떻게 정하는 것일까??
결론은 "불순도" 와 "정보획득" 을 이용한다.
불순도 (Impurity)
여기서 모든 노드들에서 확인할 수 있는 "gini 불순도", 혹은 "entropy" 를 구하고, 모델은 이를 최소화하도록 학습된다. 즉, 분기를 하였을 때 "gini 불순도", 혹은 "entropy" 가 줄어드는 방향으로 트리를 형성해야 한다.
여기서 "불순도" 란 데이터가 얼마나 섞여 있는지를 나타낸다. 즉, 정답이 아닌 다른 class가 뽑일 확률 이라고도 할 수 있다.
한 개의 class로만 데이터가 분류되었을 때 불순도는 0으로 측정되고, 여러 class가 섞일수록 불순도는 높아진다.
연산의 시간복잡도 때문인지는 모르겠으나, 보통 gini 불순도를 사용한다.

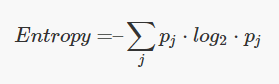
정보획득 (Information gain)
분기 이전의 불순도와 분기 이후의 불순도의 차이를 "정보획득" 이라고 한다.
만약 불순도가 1인 상태에서 0.7인 상태로 바뀌었다면 정보 획득(information gain)은 0.3이다.
트리 빌드 알고리즘
- Root 노드의 불순도 계산
- 나머지 속성에 대해 분할 후 자식노드의 불순도 계산
- 각 속성에 대한 Information Gain 계산 후 Information Gain(Root노드와 자식노드의 불순도 차이)이 최대가 되는 분기조건을 찾아 분기
- 모든 leaf 노드의 불순도가 0이 될때까지 2,3을 반복 수행.
위 단계를 따라 의사결정트리를 생성하면 모든 leaf node가 불순도 0인 (순도 100%) 인 최대 트리를 형성하게 된다.
이러한 최대 트리는 새로운 데이터가 들어왔을 때 일반화 성능이 떨어지는 overfitting 문제를 야기한다. 이를 해결하기 위해 가지치기 (pruning) 기법을 적용한다.
가지치기 (Pruning)
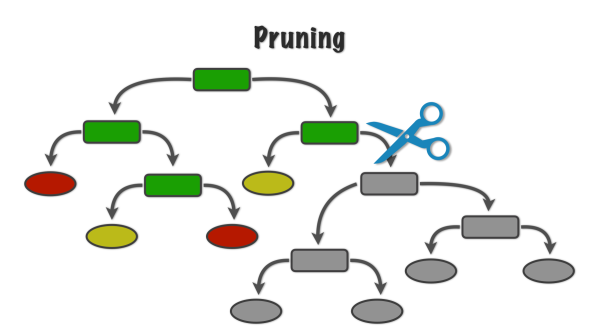
가지치기란 최대트리로 형성된 결정트리의 특정 노드 밑의 하부 트리를 제거하여 일반화 성능을 높히는 것이다.
왜 하부 트리를 제거하면 일반화 성능이 높아질까?
- 노이즈 제거:
- 최대 트리(Maximal Tree)는 학습 데이터를 완벽히 분류하려고 시도하면서, 데이터에 포함된 노이즈까지 학습하게 된다.
- 가지치기를 통해 학습 데이터에 과하게 의존하는 복잡한 분류 경로를 제거함으로써 노이즈를 줄이고, 더 단순한 모델을 만든다.
- 모델 복잡도 감소:
- 트리의 깊이가 깊어지면 모델 복잡도가 증가하고, 학습 데이터에만 잘 맞는 고분산 모델이 생성될 가능성이 커진다.
- 가지치기를 통해 복잡도를 줄이면, 모델이 새로운 데이터에 대해 더 안정적인 저분산 모델이 된다.
- 불필요한 분기 제거:
- 학습 데이터에만 의미 있는 불필요한 분기(leaf)를 제거하면, 더 일반적인 의사결정 기준을 가진 모델을 생성할 수 있다.
- 이를 통해 데이터의 본질적인 패턴만 학습하도록 유도한다.
의사결정트리는 아래와 같은 비용함수를 최소로 하는 분기를 찾아내도록 학습된다
- CC(T) = Err(T) + α × L(T)
- CC(T)
- 의사결정나무의 비용 복잡도
- 오류가 적으면서 terminal node 수가 적은 단순한 모델일 수록 작은 값
- ERR(T)
- 검증데이터에 대한 오분류율
- L(T)
- terminal node의 수
- 구조의 복잡도
- Alpha
- ERR(T)와 L(T)를 결합하는 가중치
- 사용자에 의해 부여됨, 보통 0.01~0.1의 값을 씀
- CC(T)
한계점
1. 과적합(Overfitting)
- Decision Tree는 훈련 데이터에 너무 잘 맞도록 학습하는 경향이 있다. 트리의 깊이가 너무 깊어지면 노이즈나 작은 변동까지 학습하여, 테스트 데이터에서 성능이 저하된다.
2. 불안정성(Instability)
- 데이터의 작은 변화(예: 데이터의 샘플 순서)에도 트리의 구조가 크게 바뀔 수 있다.
3. 편향된 데이터에 대한 취약성
- 데이터에 클래스 불균형이 있거나, 특정 특징이 다른 특징보다 지배적인 경우(Tree Splitting 과정에서 지배적 특징을 계속 선택), 의사결정 트리는 편향된 결과를 낼 수 있다.
4. 고차원 데이터 처리의 한계
- Decision Tree는 특징(feature)이 매우 많은 경우(고차원 데이터) 성능이 저하될 수 있다. 각 분기에서 모든 특징을 평가하므로 연산 비용이 커진다.
5. 추론 결과의 부드러움 부족
- Decision Tree는 계단식으로 결과를 추론하므로, 연속적인 데이터에서는 결과가 부드럽지 않을 수 있다.
이러한 한계점을 극복하고자 고안된 것이 다수의 의사결정트리를 결합하는 앙상블 기법인 "Random Forest" 이다.
'AI' 카테고리의 다른 글
| SVM (Support Vector Machine) 이란? (0) | 2024.11.27 |
|---|---|
| 랜덤 포레스트 (Random Forest) (0) | 2024.11.27 |
| [pytorch] 순환신경망 (Recurrent Neural Network) 예제 코드 (0) | 2024.11.21 |
| [pytorch] 합성곱 신경망 (Convolution Neural Network) 예제 코드 (0) | 2024.11.20 |
| [pytorch] 심층신경망 (Deep Neural Network) 예제 코드 (0) | 2024.11.19 |
