SVM (Support Vector Machine) 이란?

SVM은 전통적인 ML 기법 중 하나로 분류되며 이진 분류를 위해 사용된다.

 

https://ko.wikipedia.org/wiki/서포트_벡터_머신

 

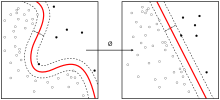
간단히 말하면, SVM은 서로 다른 클래스를 분리하기 위한 "국경 긋기 방법"이다.

 

https://ankitnitjsr13.medium.com/math-behind-svm-support-vector-machine-864e58977fdb

 

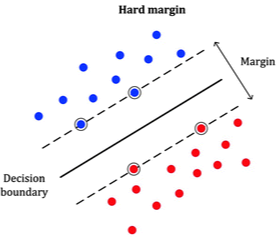
그럼 국경 (Decision boundary) 을 어떻게 그어야 할까?

 

자기 집 앞이 DMZ가 되지 않도록 모두가 만족하게 그어야 할 것이다. 이렇게 하기 위해서는 파란색 데이터에서 국경까지의 거리와 빨간색 데이터에서 국경까지의 거리가 동일해야 한다.

 

국경 (Decision boundary) 까지의 거리를 우리는 "Margin" 이라고 명칭하고,  데이터마다 Margin이 같도록, global한 관점에서 봤을 때는 Margin이 크도록 국경을 긋게 된다.

 

 

이 국경을 좌표평면에서 수식으로 표현하면,

 

$ax+by=c$ 이고 이를 행렬로 나타내면,

 

$ \begin{bmatrix} a & b \\ \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} =c$ 와 같이 나타낼 수 있다.

 

$\underline{w}\overset{\underset{\mathrm{def}}{}}{=}\begin{bmatrix} a \\ b \end{bmatrix}$ , 

 

$\underline{d}\overset{\underset{\mathrm{def}}{}}{=}\begin{bmatrix} x \\ y \end{bmatrix}$ 라고 한다면, 위 식은 

 

$\underline{w}^{T}\underline{d}=\left\| \underline{w} \right\|\left\| \underline{d} \right\|\cos{\theta}=c$ 로 나타낼 수 있다.

 

위 수식에서 알 수 있듯, $\underline{d}$ 의 자취는 직선이 된다.

 

다시 국경 긋기로 돌아오면, 

 

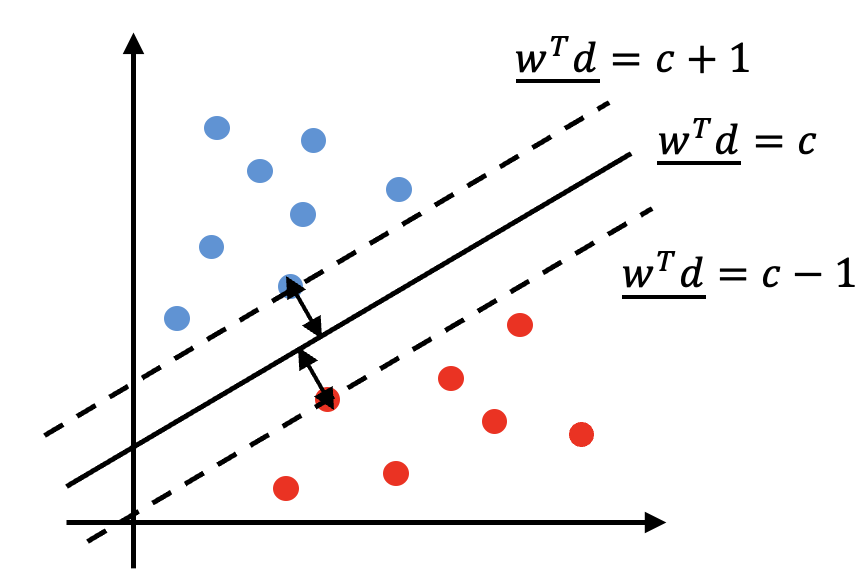
위 문제에서 margin을 최대화 하면 되는 것이고 이는 $\frac{2}{\left\|\underline{w}\right\|}$ 로 나타낼 수 있다. 이걸 최대화 하면 된다!

 

이걸 최소화 문제로 바꿔서 나타내면, $\frac{1}{2}\underline{w}^{T}\underline{w}$를 최소화 하는 문제로 바꿀 수 있고, 파란색, 빨간색 데이터가 각각의 점선 위에 위치해야 하므로..

 

• $\underline{w}^{T}\underline{d_{i}}\geq c+1$, (i는 파란색)
• $\underline{w}^{T}\underline{d_{i}}\leq  c-1$, (i는 빨간색)

 

위 두 수식을 영차영차 .. 잘 해서 미분을 구하고 해결하면 된다.