선형 회귀 (Linear Regression)

해당 게시물은 "혁펜하임의 AI DEEP DIVE"를 수강하고 작성되었습니다.

---

딥러닝을 하다 보면 "회귀"라는 말이 굉장히 많이 사용된다.

 

회귀란,  "입력과 출력 간의 관계를 추정하는 것" 이다.

 

선형 회귀는 "입력과 출력 간의 관계를 선형으로 놓고 추정하는 것" 이다.

 

 

https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%ED%9A%8C%EA%B7%80

 

 

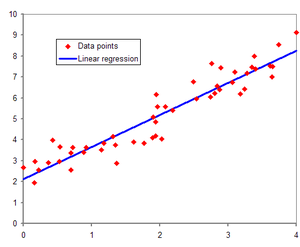
대표적인 선형 방정식인 $ax+b$에서 $a$는 weight(곱해지는 것, 중요도)이며 $b$는 bias(더해지는 것, 민감도)이다.

 

이때 weight와 bias 즉, a와 b를 잘 추정한다면 내가 모르는, 새롭게 들어오는 입력 x에 대해서도 적절한 출력을 낼 수 있지 않을까? 하는 것이다.

 

선형 회귀는 ML에 속하는 지도학습 방법이다. 인공지능과 ML의 경계를 구분하는 것은 데이터 기반인가? 이므로 선형 회귀는 데이터를 기반으로 weight와 bias를 추정한다.

 

내가 추정한 weight와 bias는 loss function으로 좋은지 나쁜지 판단한다. 즉, loss function을 최소화 하는 방향으로 weight와 bias를 찾고자 하게 된다.

 

 

 

---

 

 

loss함수의 종류 중 MSE (Mean Squared Error)는 예측값과 실체값의 오차 정도에 민감하게 반응하고자 절댓값 대신 $(실제 값-예측값)^2$과 같이 제곱하는 방법을 택한다. 

 

MSE를 최소화 하는 a, b는 어떻게 찾을까? -> 경사 하강법